数列极限的定义
引例
给定一个数列 {n+1n} ,他的每一项是: 21 , 32 , 43 , … , n+1n , … , 随着 n 无限增大, n+1n 无限趋于 1 。
设 ϵ=101 ,当 n>9 时, n+1n−1<ϵ
设 ϵ=1001 ,当 n>99 时, n+1n−1<ϵ
设 ϵ=1001 ,当 n>999 时, n+1n−1<ϵ
…
可以推测,无论 ϵ 取多小,都能找到 N>0 ,当 n>N 时,数列 {n+1n} 与 1 的差距都小于 ϵ 。也就是说,从某项之后,该数列的所有项都会**更接近 1 **。
定义
ϵ - N 语言
设 {xn} 为一数列,若存在常数 a ,对于任意的 ϵ>0 (无论他多么小),总存在 N>0 ,使得当 n>N 时,
∣xn−a∣<ϵ
恒成立,
则称数 a 是数列 {xn} 的极限,或称数列 {xn} 收敛于 a ,记为
n→∞limxn=a 或 xn→a(n→∞)
若存在这样的 a ,则称数列是收敛的,否则称之为发散的。
- 序号 N 的确定,依赖于 ϵ 的选择,常记为 N(ϵ) 。 xa 的值与常数 a 的值越接近( ϵ 越小),就必须在数列中考虑越远( N 越大)的数值。
- N 不需要是整数,因为 n 是正整数,当 n>N 时,总有 n⩾[N]+1
单调数列和严格单调数列
如果数列 {xn} 满足
xn⩽xx+1,n=1,2,3,...,
则称 {xn} 为单调增加数列;若进一步满足
xn<xn+1,n=1,2,3,...,
则称 {xn} 为严格单调增加数列。
可以类似的定义单调减少函数和严格单调减少函数。
收敛数列的性质
收敛数列的唯一性
设数列an 是收敛的,且n→∞liman=A ,n→∞liman=B,证明:A=B 。
证明:假设A>B ,取ϵ=2A−B由于n→∞liman=A有 ∃N1>0 ,当n>N1时,∣an−A∣<ϵ即 2A+B<an<23A−B(∗)又 n→∞liman=B有 ∃N2>0 ,当 n>N2时,∣an−B∣<ϵ即 23B−A<an<2A+B(∗∗)取 N=max{N1,N2} ,当n>N时,(∗)、(∗∗) 皆成立由此得到矛盾,所以 A>B 不成立同理可得 A<B 不成立因此 A=B
收敛数列的有界性
设数列 {an} 收敛于A, 证明:存在 M>0,使得 {an}≤M 。
证明:取ϵ=1根据题设,n→∞liman=A ,有 ∃N>0 ,当n>N时∣an−A∣<1⟹∣an∣<1+∣A∣取 M=max{∣a1∣,∣a2∣,…,∣an∣,1+∣A∣}则,对于任意的 n ,有 {an}≤M
收敛数列的保序性
设数列 {an},{bn} 均收敛,若 n→∞liman=A ,n→∞limbn=B ,且 A<B ,则存在正整数N,当n>N时,成立 an<bn 。
证明:取ϵ=2B−A由n→∞liman=A ,∃N1>0 ,当n>N1 时 ∣an−A∣<2B−A ,因而an<2A+B而由n→∞limbn=B ,∃N2>0 ,当n>N2 时 ∣bn−B∣<2B−A ,因而bn>2A+B取 N=max{N1,N2} ,∀n>N: an<2A+B<bn
几何意义:
liman>b,∃N>0,∀n>N,an>b(1)
liman<a,∃N>0,∀n>N,an<a(2)
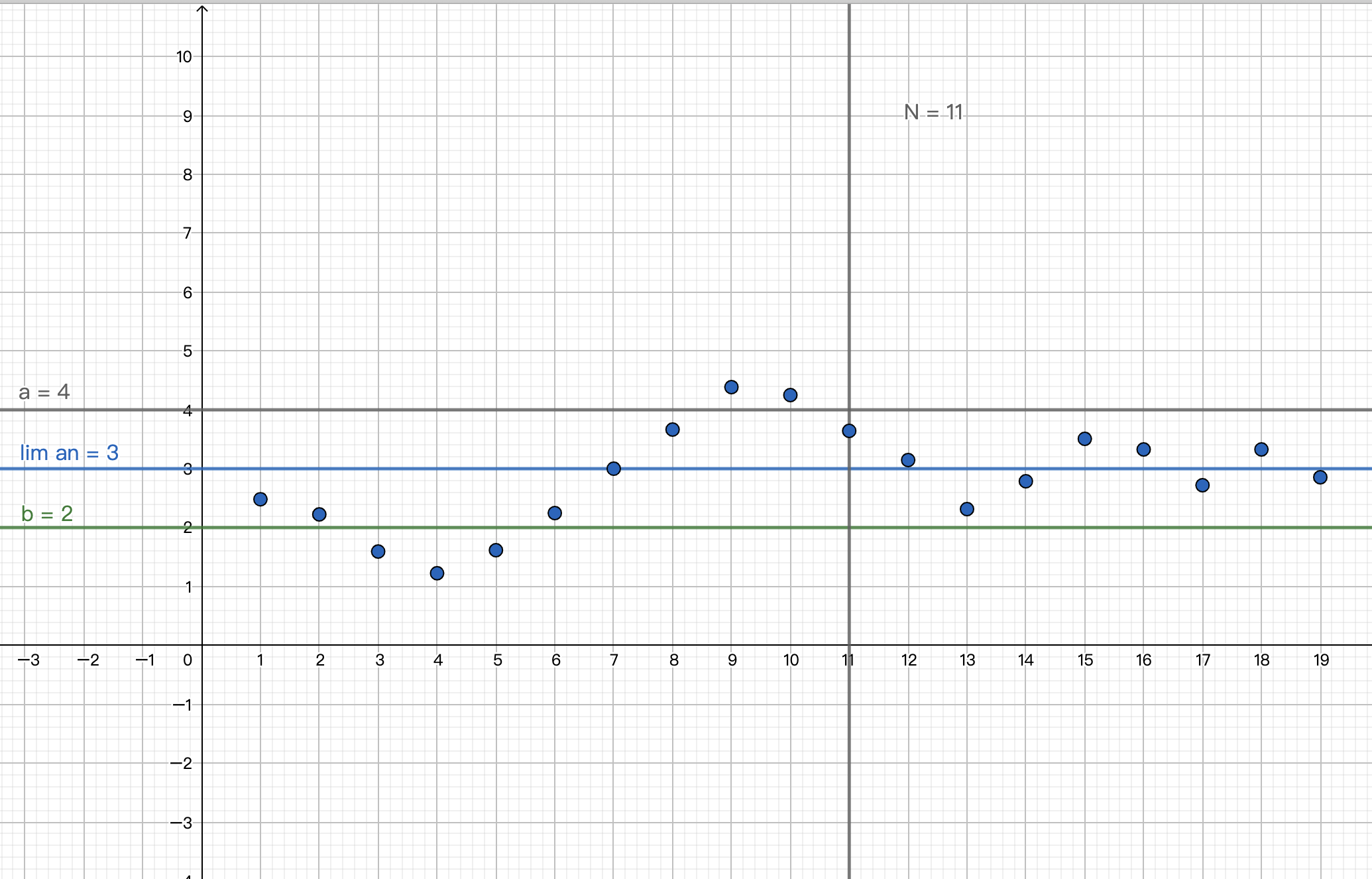
收敛数列的保序性的推论
(1) 若 n→∞liman=A>0 ,则存在正整数 N ,当 n>N 时,
an>2A>0.
(2) 若 n→∞liman=A<0 ,则存在正整数 N ,当 n>N 时,
an<2A<0.
子列
设 {xn} 是一个数列,而
n1<n2<⋯<nk<nk+1<⋯
是一个严格单调增加的正整数,则
xn1,xn2,⋯,xnk,⋯
也形成一个数列,称为数列 {xn} 的子列,记为 {xnk} 。
子列收敛定理
若数列 {xn} 收敛于 a ,则它的任何子列 {xnk} 也收敛于 a ,即
n→∞limxn=a⟹n→∞limxnk=a。
证明:由n→∞limxn=a ,可知 ∀ϵ>0 , ∃N , ∀n>N 有: ∣xn−a∣<ϵ 。取 K=N ,于是当 k>K 时,有 nk⩾k>N ,因而成立∣xnk−a∣<ϵ 。
子列收敛定理的推论
若数列 {xn} 的两个子列 {xnk(1)} 和 {xnk(2)} 收敛于不同的极限,则数列 {xn} 必定发散。
夹逼准则
若三个数列{xn}、{yn}、{zn} ,从某项开始成立
xn⩽yn⩽zn ,n>N0 ,
且n→∞limxn=n→∞limzn=a,则
n→∞limyn=a。
夹逼准则不验证等号
证明:∀ϵ>0 ,由 n→∞limxn=a ,可知 ∃N1 ,∀n>N1 有 ∣xn−a∣<ϵ ,从而有a−ϵ<xn由 n→∞limzn=a ,可知 ∃N2 ,∀n>N2 有 ∣zn−a∣<ϵ ,从而有zn<a+ϵ取N=max{N0,N1,N2} ,∀n>N ,有a−ϵ<xn⩽yn⩽zn<a+ϵ ,此即∣yn−a∣<ϵ
证明:不妨设数列 {xn} 单调增加且有上界,根据确界存在定理,由 {xn} 构成的数集必有上确界 β,取 N=n0 ,∀n>N ,有:β−ϵ<xn0⩽xn⩽β因而 ∣xn−β∣<ϵ ,于是得到n→∞limxn=β
同理可证单调减少且有下界的数列,必定收敛。
闭区间套
如果一列闭区间 {[an,bn]} 满足
(1). [an+1,bn+1]⊂[an,bn],n=1,2,3,⋯ ;
(2). n→∞lim(bn−an)=0 ,
则称这列闭区间形成一个闭区间套。
闭区间套定理
如果 {[an,bn]} 形成一个闭区间套,则存在唯一实数 ξ 属于所有的闭区间 [an,bn] ,且 ξ=n→∞liman=n→∞limbn 。
证明: 由条件(1)可得
a1⩽⋯≤an−1⩽an<bn⩽bn−1⩽⋯⩽b1.
显然 {an} 单调增加且有上界 b1 。 {bn} 单调减少且有下界 a1 ,由单调有界准则, an 与 bn 都收敛。
设 n→∞liman=ξ ,则
n→∞limbn=n→∞lim[(bn−an)+an]=n→∞lim(bn−an)+n→∞liman=ξ.
由于 ξ=sup{an}=inf{bn} ,于是有
an⩽ξ⩽bn,n=1,2,3,⋯,n=1,2,3,⋯,
即 ξ 属于所有闭区间 {[an,bn]} 。
若另有实数 ξ′ 属于所有闭区间 {[an,bn]} ,则也有
an⩽ξ′⩽bn,n=1,2,3,⋯,n=1,2,3,⋯,
令 n→∞ ,由夹逼定理得到
ξ′=n→∞liman=n→∞limbn=ξ,
即 ξ 是唯一的。
基本列
设数列 {xn} ,∀ϵ>0 ,∃N>0 ,当 n,m∈N∗ 且 m,n>N 时,成立:
∣xn−xm∣<ϵ,
则称数列 {xn} 是一个基本数列或Cauchy列。
基本列的特征是,数列中充分靠后的两项,无论相对位置如何,他们的差都小于任一事先给定的程度。
有界数列必有收敛子列
波尔查诺-魏尔斯特拉斯(Bolzano - Weierstrass)定理:有界数列必有收敛子列。
证明:
(1). 设数列 {xn} 有界,于是存在实数 a1,b1 ,成立
a1⩽xn⩽b1,n=1,2,3,⋯
将闭区间 [a1,b1] 等分为两个小区间 [a1,2a1+b1] 与 [2a1+b1,b1] ,则其中至少有一个含有数列 {xn} 中的无穷多项,记为 [a2,b2] 。
再将闭区间 [a2,b2] 等分为两个小区间 [a2,2a2+b2] 与 [2a2+b2,b2] ,同样其中至少有一个含有数列 {xn} 中的无穷多项,记为 [a3,b3] 。
⋯
于是得到一个闭区间套 {[ak,bk]} ,其中每一个闭区间 [ak,bk] 中都含有数列 {xn} 中的无穷多项。
根据闭区间套定理,存在实数 ξ ,满足
ξ=k→∞limak=k→∞limbk.
(2). 首先在 [a1,b1] 中选取 {xn} 中的某一项,记为 xn1 。
由于 [a2,b2] 中含有 {xn} 中的无穷多项,在其中取 xn1 后的某一项记为 xn2 ,其中 n2>n1 。
⋯
选取 xnk∈[ak,bk] 后,因为在 [ak+1,bk+1] 中仍含有 {xn} 中的无穷多项,在其中选取 xnk 后的某一项,记为 xnk+1 ,其中 nk+1>nk 。
于是得到数列 {xn} 的一个子列 {xnk} ,满足
ak⩽xnk⩽bk,k=1,2,3,⋯
由 k→∞limak=k→∞limbk=ξ ,利用极限的夹逼性,得到
k→∞limxnk=ξ.
当数列无界时,也有相应的结论:
若 {xn} 是一个无界数列,则存在子列 {xnk} ,使得
k→∞limxnk=∞.
Cauchy收敛原理
数列收敛的充分必要条件是该数列是基本数列。此定理称为Cauchy收敛原理。
Stolz 定理
设 {yn} 是严格单调增加的正无穷大量,且
n→∞limyn−yn−1xn−xn−1=a(a 为有限量, +∞ 与 −∞ ),
则
n→∞limynxn=a.
