**例：当 $x \to 0$ 时，函数 $x[\dfrac{1}{x}]+ e^\frac{1}{x}$ 的极限 $(\qquad)$**

$\begin{aligned} &\text{由于 } \dfrac{1}{x} - 1 \lt [\dfrac{1}{x}] \leqslant \dfrac{1}{x} : \\\\ &\text{当 } x \to 0^+ \text{ 时，有} 1-x \lt x[\dfrac{1}{x}] \leqslant 1, \\\\ &\text{根据夹逼定理得：} \lim\limits_{x \to 0^+} x[\dfrac{1}{x}] = 1 , \text{ 即， } \lim\limits_{x \to 0^+} x[\dfrac{1}{x}]+ e^\frac{1}{x} = +\infty , \\\\ &\text{当 } x \to 0^- \text{ 时，有} 1 - x \gt x[\dfrac{1}{x}] \geqslant 1, \\\\ &\text{根据夹逼定理得：} \lim\limits_{x \to 0^-} x[\dfrac{1}{x}] = 1 , \text{ 即， } \lim\limits_{x \to 0^-} x[\dfrac{1}{x}]+ e^\frac{1}{x} = 1 , \\\\ &\text{函数的左右极限不相等，因此，当 } x \to 0 \text{ 时，函数 } x[\dfrac{1}{x}]+ e^\frac{1}{x} \text{ 的极限不存在。} \end{aligned}$

$$ \begin{aligned} & \text{证明：} \\\\ & \forall \epsilon > 0 \text{ ，} \\\\ & \exists \delta_1 > 0 \text{ ， } \forall x (0 < \lvert x - x_0 \rvert < \delta_1) \text{ ：} \lvert f(x) - A \rvert < \epsilon \text{ ， } \\\\ & \exists \delta_2 > 0 \text{ ， } \forall x (0 < \lvert x - x_0 \rvert < \delta_2) \text{ ：} \lvert f(x) - B \rvert < \epsilon \text{ ， } \\\\ & \text{取 } \delta = \min\{\delta_1, \delta_2\} \text{ ， } \forall x (0 < \lvert x - x_0 \rvert < \delta) \text{ ： } \\\\ & \lvert A - B \rvert <\lvert f(x) - A \rvert + \lvert f(x) - B \rvert < 2\epsilon \quad\text{。} \\\\ & \text{ 由于 } \epsilon \text{是任意接近于 0 ，因此 } A= B \quad\text{。} \end{aligned} $$

$$ \begin{aligned} & \text{证明：} \\\\ & \text{取} \epsilon = \dfrac{A - B}{2} > 0 \quad\text{。} \\\\ & \text{由} \lim\limits_{x \to x_0}f(x) = A \text{，} \exists \delta_1 \text{，} \forall x ( 0 < \lvert x - x_0 \rvert < \delta_1 ) : \\\\ & \lvert f(x) - A \rvert < \dfrac{A - B }{2} \text{ 即 } f(x) > \dfrac{A + B}{2} \qquad\qquad (1) \\\\ &\text{又} \lim\limits_{x \to x_0} g(x) = B \text{，} \exists \delta_2 \text{，} \forall x ( 0 < \lvert x - x_0 \rvert < \delta_2 ) : \\\\ & \lvert g(x) - B \rvert < \dfrac{A - B }{2} \text{ 即 } g(x) < \dfrac{A + B}{2} \qquad\qquad (2) \\\\ & \text{取} \delta = \min \{\delta_1, \delta_2 \} \text{，当} 0 < \lvert x - x_0 \rvert < \delta \text{时，} (1)\text{、}(2) \text{皆成立，即：} \\\\ \end{aligned} $$

$g(x) < \dfrac{A + B}{2} < f(x) \quad\text{。}$

$\begin{aligned} & \text{证明：} \\\\ & \text{取常数 } M \text{ 与 } m \text{ ，满足 } m \lt A \lt M \text{ ，令 } g(x) = m , h(x) = M \text{ 为两个常函数，} \\\\ & \text{由局部保序性 } \text{ 可知，} \exists \delta \gt 0 \text{ ，当 } 0 \lt \lvert x - x_0 \rvert \lt \delta \text{ 时，成立} \\\\ & \quad\quad\quad\quad m \lt f(x) \lt M \quad \text{。} \end{aligned}$

$$ \begin{aligned} & \Large\text{证明：} \\\\ & \forall \epsilon \gt 0, \text{ 由 } \lim\limits_{x \to x_0}{h(x)} = A, \text{ 可知 } \exists \delta_1 \gt 0, \\\\ & \forall x (0 \lt \lvert x - x_0 \rvert \lt \delta_1): \lvert h(x) - A \rvert \lt \epsilon , \text{ 从而，} h(x) \lt A + \epsilon; \\\\ & \text{由 } \lim\limits_{x \to x_0}{g(x)} = A, \text{ 可知 } \exists \delta_2 \gt 0, \\\\ & \forall x (0 \lt \lvert x - x_0 \rvert \lt \delta_2): \lvert g(x) - A \rvert \lt \epsilon , \text{ 从而，} A - \epsilon \lt g(x); \\\\ & \text{取 } \delta = min\{\delta_1, \delta_2, r\} , \forall x (0 \lt \lvert x - x_0 \rvert \lt \delta) : A - \epsilon \lt g(x) \leqslant f(x) \leqslant h(x) \lt A + \epsilon , \\\\ & \text{即 } \lim\limits_{x \to x_0}{f(x)} = A \end{aligned} $$

$$ \begin{aligned} & \text{证明：} \\\\ & \text{ 必要性：} \\\\ & \text{由 } \lim\limits_{x \to x_0} f(x) = A \text{ ，可知， } \forall \epsilon \gt 0, \exists \delta \gt 0 , \forall x (0 \lt \lvert x - x_0 \rvert \lt \delta): \\\\ & \quad\quad\quad\quad \lvert f(x) - A \rvert \lt \epsilon \quad \text{ 。} \\\\ & \text{因为 } \lim\limits_{n \to \infty} x_n = x_0 \text{ ，且 } x_n \neq x_0 (n = 1, 2, 3, ...) \text{ ，对于上述 } \delta \gt 0 , \exists N , \forall n \gt N : \\\\ & \quad\quad\quad\quad 0 \lt \lvert x_n - x_0 \rvert \lt \delta \quad \text{ 。} \\\\ & \text{于是当 } n \gt N \text{ 时，成立} \\\\ & \quad\quad\quad\quad \lvert f(x_n) - A \rvert \lt \epsilon \quad \text{ ，} \\\\ & \text{即 } \lim\limits_{n \to \infty} f(x_n) = A \quad\text{ 。} \\\\ & \text{ 充分性：} \\\\ & \text{由于 } \lim\limits_{x \to x_0} f(x) = A \text{ ，即： } \forall \epsilon \gt 0 , \exists \delta \gt 0 , \forall x (0 \lt \lvert x - x_0 \rvert \lt \delta) : \lvert f(x) - A \rvert \lt \epsilon \\\\ & \text{其否定命题 } \lim\limits_{x \to x_0} f(x) \neq A \text{ ，即： } \exists \epsilon_0 \gt 0, \forall \delta \gt 0, \exists x (0 \lt \lvert x - x_0 \rvert \lt \delta) : \lvert f(x) - A \rvert \geqslant \epsilon_0 \end{aligned} $$

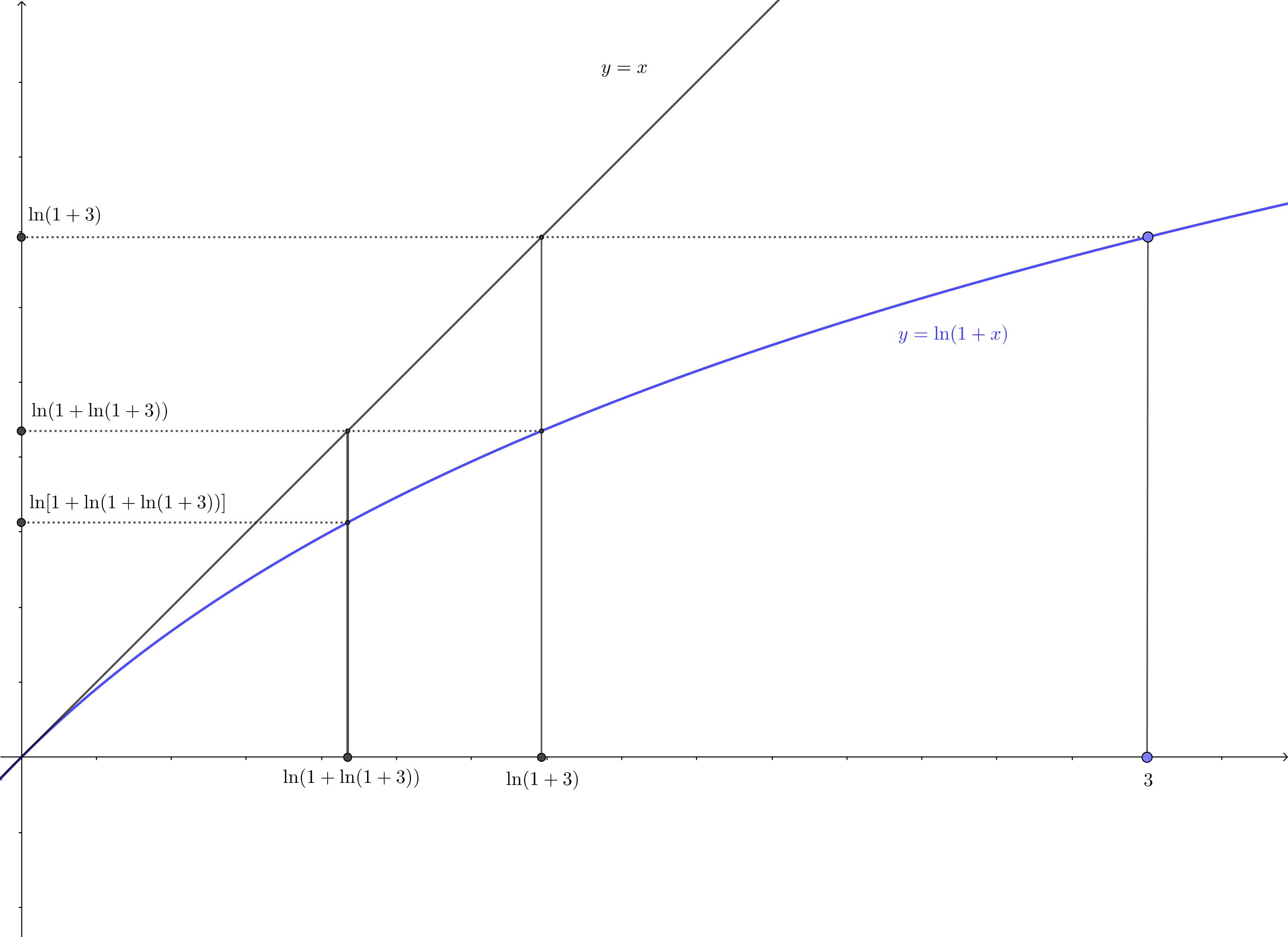
例：设 $a_1 \gt 0$ ， $\{a_n\}$ 满足 $a_{n+1} = \ln (1+a_n), n=1,2,\cdots.$

（1）证明 $\lim\limits_{n \to \infty}a_n$ 存在，并求其值；

（2）求 $\lim\limits_{n \to \infty} \dfrac{a_{n+1}a_n}{a_n - a_{n+1}}$

$\begin{aligned} (1)& \\\\ & \text{由 } a_1 \gt 0 \text{ ，设 } a_{k-1} \gt 0 \text{ ，则 } a_k = \ln(1+a_{k-1}) \gt 0 \text{ ，故 } \{a_n\} \text{ 有下界} 0. \\\\ & \text{当 } x_n \gt 0 \text{ 时， } a_{n+1} = ln(1+a_n) \lt a_n , \\\\ & \text{于是 } \{x_n\} \text{ 单调减少，由单调有界准则， } \lim\limits_{n \to \infty} a_n \text{ 存在。} \\\\ & \text{记 } \lim\limits_{n \to \infty} a_n = a \text{ ，根据递推式，得} a = \ln(1+a) \text{ ，解得 } a = 0. \\\\ (2)& \\\\ & \lim\limits_{n \to \infty} \dfrac{a_{n+1}a_n}{a_n-a_{n+1}} \\\\ & = \lim\limits_{n \to \infty} \dfrac{a_n\ln(1+a_n)}{a_n - \ln(1+a_n)} \\\\ & = \lim\limits_{x \to 0^+} \dfrac{x\ln(1+x)}{x - \ln(1+x)} \qquad\qquad (*) \\\\ & = \lim\limits_{x \to 0^+}\dfrac{x^2}{\frac{1}{2}x^2} \qquad\qquad\qquad\qquad (**)\\\\ & = 2. \end{aligned}$

$(*)$ ：归结原则： $x_n \to a,\lim\limits_{x \to a}f(x) = A \Rightarrow \lim\limits_{n \to \infty}f(x_n)=A$

$(**)$ ：$\ln(1+x) = \ x - \dfrac{1}{2}x^2 + o(x^2) \Rightarrow x - \ln(1+x) \sim \dfrac{1}{2}x^2$