引例

1. 平均变化率

在一个普通的室内，假设在$t=9:00$时，温度为$u=20 \degree C$，$\tilde{t}=9:05$时，温度为$\tilde{u}=25\degree C$，则在着$5min$里室内温度的平均变化率为：

$\frac{\Delta u}{\Delta t} = \frac{\tilde{u} - u}{\tilde{t} - t}=1(\degree C/min)$

不过，平均变化率并不能真实的反应一段时间的变化情况。如：现在这个时刻$t$，室温$u=20\degree C$，一年之前$\tilde{t}$时刻，温度$\tilde{u}=20\degree C$，则其平均变化率为$0(\degree C/min)$，但并不能说这一年，温度没有变化。这种只看“两头”的研究方式非常粗糙，不能说明在某一个瞬时温度的变化。
当我们让平均变化率中的时间间隔趋于$0$，便能得出在这一时刻的变化情况：

$\lim\limits_{\Delta t\to 0}\frac{\Delta u}{\Delta t}$

2. 切线及其斜率

如图下图所示，当点$M1$沿着曲线$K$向$M$点靠近时，割线$MM1$的极限位置$MT$就叫做曲线$K$在点$M$处的切线。

又如下图所示：

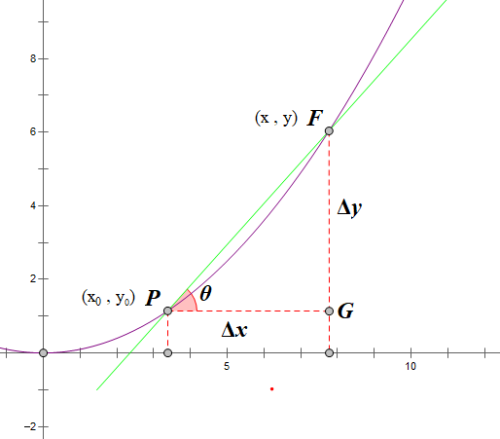
割线$PF$的斜率为

$\tan\theta = \frac{y-y_0}{x-x_0} = \frac{f(x)-f(x_0)}{x-x_0}$

其中$\theta$为割线的$PF$的倾角。
当点$F$沿着曲线无限接近于$P$点时，割线斜率的极限值：

$\lim\limits_{x \to x_0}\frac{f(x)-f(x_0)}{x-x_0}$

就是点$P$的切线的斜率。曲线在点 $P(x_0, y_0)$ 的切线方程为：

$y-y_0 = f \rq (x_0)(x-x_0)$

这两个引例的本质都是计算当自变量增量趋于$0$时，函数增量与自变量增量比值的极限。由此引出了导数的定义

定义

设函数$y=f(x)$在区间$I$上有定义。从自变量的某一数值$x=x_0$开始，加一个增量$\Delta x \gtrless 0$（其中$x+\Delta x \in I$），则函数的增量为

$\Delta y=f(x_0+\Delta x)-f(x_0).$

令$\Delta x = x - x_0$，则导数定义又可写成

$f \rq (x)=\lim\limits_{x \to x_0}\frac{f(x)-f(x_0)}{x-x_0}$

单侧导数

当函数的自变量趋于一点时，可以从定义区间的左侧或右侧趋向于该点。

函数在一点可导，当且仅当在该点的左右导数都存在且相等。

导数的运算法则

加法法则

设 $f(x)$ 和 $g(x)$ 在某一区间上都是可导的，则对任意常数 $c_1$ 和 $c_2$ ，他们的线性组合 $c_1f(x) + c_2g(x)$ 也在该区间上可导，且：

$[c_1f(x) + c_2g(x)] \rq = c_1f \rq (x) + c_2g \rq (x)$

$\begin{aligned} \text{证明：} &\\\\ &\text{由于 } f(x) \text{ 和 } g(x) \text{ 在区间上是可导的，可得} \\\\ &[c_1f(x)+c_2g(x)] \rq \\\\ & = \lim\limits_{\Delta x \to 0}\dfrac{[c_1f(x+\Delta x) + c_2g(x + \Delta x)] - [c_1f(x) + c_2g(x)]}{\Delta x} \\\\ & = c_1 \cdot \lim\limits_{\Delta x \to 0} \dfrac{f(x + \Delta x) - f(x)}{\Delta x} + c_2 \cdot \lim\limits_{\Delta \to 0}\dfrac{g(x + \Delta x) - g(x)}{\Delta x} \\\\ & = c_1f \rq (x) + c_2g \rq (x) \end{aligned}$

该结论可推广至多个函数线性组合的情况：

$[\displaystyle\sum_{i=1}^{n}c_i f_i(x)]\rq = \displaystyle\sum_{i=1}^{n}c_i f_i\rq (x)$

乘法法则

设 $f(x)$ 和 $g(x)$ 在某一区间上都是可导的，则他们的积函数也在该区间上可导，且：

$[f(x) \cdot g(x)] \rq = f \rq (x)g(x) + f(x)g \rq (x)$

@todo 证明

该结论可推广至多个函数乘积的情况：

$[\displaystyle\prod_{i=1}^{n} f_i (x)]\rq = \displaystyle \sum_{j=1}^{n}\{f_j\rq (x)\displaystyle\prod_{i=1,i\neq j}^{n}f_i(x)\}$

只有在可导的点才能用乘法法则，在不成立的点需要用定义法。

倒数法则

设 $g(x)$ 在某一区间上可导，且 $g(x) \neq 0$ ，则它的倒数也在该区间上可导，且满足：

$[\dfrac{1}{g(x)}] \rq = - \dfrac{g\rq (x)}{[g(x)]^2}$

$\begin{aligned} &\text{证明：} \\ [\dfrac{1}{g(x)}]\rq & = \lim\limits_{\Delta x \to 0}\dfrac{\dfrac{1}{g(x+\Delta x)} - \dfrac{1}{g(x)}}{\Delta x} \\\\ &=\lim\limits_{\Delta x \to 0}\dfrac{g(x) - g(x + \Delta x)}{g(x+\Delta x)\cdot g(x) \cdot \Delta x}\\\\ &=\dfrac{-1}{g(x)}\cdot (\lim\limits_{\Delta x \to 0}\dfrac{g(x + \Delta x) - g(x)}{\Delta x}) \cdot (\lim\limits_{\Delta x \to 0}\dfrac{1}{g(x + \Delta x)})\\\\ &=\dfrac{-1}{g(x)}\cdot g\rq (x) \cdot \dfrac{1}{g(x)} \\\\ &=-\dfrac{g\rq (x)}{[g(x)]^2} \end{aligned}$

由此可得除法的导数 $(\dfrac{f(x)}{g(x)}) \rq = \dfrac{f\rq (x) \cdot g(x) - f(x) \cdot g\rq (x)}{[g(x)]^2}$

复合函数求导

设函数 $u=g(x)$ 在 $x = x_0$ 处可导，而函数 $y=f(u)$ 在 $u = u_0 = g(x_0)$ 处可导，则复合函数 $y = f(g(x))$ 在 $x = x_0$ 处可导，且：

$[f(g(x))] \rq _{x=x_0} = f\rq (u_0)g\rq (x_0) = f\rq (g(x_0))g\rq (x_0)$

复合函数的求导规则可以写成：$\dfrac{dy}{dx}=\dfrac{dy}{du}\cdot\dfrac{du}{dx}$ ，称为链式法则。

反函数求导

若函数 $y = f(x)$ 在 $(a, b)$ 内连续、严格单调、可导并且 $f\rq (x) \neq 0$ ，
记 $\alpha = \min (f(a+), f(b-)), \beta = \max(f(a+),f(b-))$ ，则它的反函数 $x = f^{-1}(y)$ 在 $(a,b)$ 上可导，且：

$[f^{-1}(y)]\rq = \dfrac{1}{f\rq(x)}$

基本求导公式

$\begin{aligned} \text{幂函数：} \\\\ (x^a) \rq &= ax^{(a-1)} \\\\ \text{指数函数：} \\\\ (a^x) \rq &= a^x\ln a \\\\ &(e^x) \rq = e^x \\\\ \text{对数函数：} \\\\ (log_a x) \rq &= \dfrac{1}{x\ln a},(a>0,a\neq 1)\\\\ &(\ln x) \rq = \dfrac{1}{x} \\\\ \text{三角函数：} \\\\ (\sin x) \rq &= \cos x \\\\ (\cos x) \rq &= -\sin x \\\\ (\tan x) \rq &= \sec ^ 2 x \\\\ (\cot x) \rq &= -\csc ^ 2 x \\\\ (\sec x) \rq &= \tan x \sec x \\\\ (\csc x) \rq &= -\cot x \csc x \\\\ \text{反三角函数：} \\\\ (\arcsin x) \rq &= \dfrac{1}{\sqrt{1-x^2}} \\\\ (\arccos x) \rq &= -\dfrac{1}{\sqrt{1-x^2}} \\\\ (\arctg x) \rq&=\dfrac{1}{1+x^2} \\\\ (\arcctg x) \rq&=-\dfrac{1}{1+x^2} \\\\ \text{其他：} \\\\ [\ln(x + \sqrt{x^2 + 1})] \rq &= \dfrac{1}{\sqrt{x^2 + 1}} \\\\ [\ln(x + \sqrt{x^2 - 1})] \rq &= \dfrac{1}{\sqrt{x^2 - 1}} \end{aligned}$

高阶导数

设函数 $y = f(x)$ 的 $n-1$ 阶导数 $f^{(n-1)}(x)$ 仍是个可导函数，则它的导数 $[f^{(n-1)}(x)]\rq$ 被称为 $f(x)$ 的 $n$ 阶导数，记为

$f^{(n)}(x)$

并称 $f(x)$ 是 $n$ 阶可导函数。

显然，若 $f(x)$ 的 $n$ 阶导数存在，则它的低于 $n$ 阶的导数都存在。

加法的高阶导数法则

设 $f(x)$ 和 $g(x)$ 都是 $n$ 阶可导的，则对任意常数 $c_1$ 和 $c_2$ ，它们的线性组合 $c_1f(x) + c_2g(x)$ 也是 $n$ 阶可导的，且满足如下的线性运算关系：

$[c_1f(x) + c_2g(x)]^{(n)} = c_1f^{(n)}(x) + c_2g^{(n)}(x)$

该结论可推广至多个函数的线性组合情况：

$[\displaystyle\sum_{i=1}^{n}c_if_i(x)]^{(n)} = \displaystyle\sum_{i=1}^{n}c_if_i^{(n)}(x)$

乘法的高阶导数法则

设 $f(x)$ 和 $g(x)$ 都是 $n$ 阶可导函数，则他们的积函数也是 $n$ 阶可导，且：

$[f(x) \cdot g(x)]\rq = \displaystyle\sum_{k=0}^{n}\complement_n^kf^{(n-k)}(x)g^{(k)}(x)$

其中，$\complement_n^k = \dfrac{n!}{k!(n-k)!}$ 是组合系数。该定理又称Leibniz公式

例题

例题1（求导后奇偶性互换）

证明：若$f (x)$是可导的偶函数，则$f \rq (x)$是奇函数

$\begin{aligned} f \rq (-x) &=\lim\limits_{\Delta x \to 0}\frac{f(-x+\Delta x)-f(-x)}{\Delta x}\\\\ &=\lim\limits_{\Delta x \to 0}\frac{f(x-\Delta x)-f(x)}{\Delta x}\\\\ &=(-1)\lim\limits_{-\Delta x \to 0}\frac{f[x+(-\Delta x)] - f(x)}{-\Delta x}\\\\ &=-f \rq (x) \end{aligned}$

同理可证：若$f (x)$是可导的奇函数，则$f \rq (x)$是偶函数。

例题2（周期函数的导数周期不变）

证明：若$f (x)$是可导的以$T$为周期的函数，则$f \rq (x)$也是以$T$为周期的函数。

$\begin{aligned} f \rq (x+T) &= \lim\limits_{\Delta x \to 0}\frac{f(x+T+\Delta x)-f(x+T)}{\Delta x}\\\\ &= \lim\limits_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}\\\\ &= f \rq (x) \end{aligned}$

例题3

设$f (x)$是二阶可导的以$2$为周期的奇函数，且$f(\frac{1}{2})>0$，$f \rq (\frac{1}{2})>0$，比较$f (-\frac{1}{2})$，$f \rq (\frac{3}{2})$与$f \rq \rq (0)$的大小。

1. 根据 函数求导后奇偶性互换有：

$\begin{aligned} & f (x) \text{是奇函数} \\\\ & \implies f \rq (x) \text{是偶函数} \\\\ & \implies f \rq \rq (x) \text{是奇函数} \\\\ &\implies \color{blue}f\rq\rq(0)=0 \end{aligned}$

2. 由于$f(x)$是奇函数，且$f(\frac{1}{2})>0$，则

$\color{blue}f(-\frac{1}{2}) \color{black}=-f(\frac{1}{2}) \color{blue}{<0}$

3. 由于$f(x)$是以$2$为周期的奇函数，则$f\rq(x)$是以$2$为周期的偶函数，于是

$\color{blue}f\rq({3 \over 2}) \color{black}=f\rq({3 \over 2}-2)=f\rq(-{1 \over 2})=f\rq({1 \over 2}) \color{blue}>0$

综上：$f\rq({3 \over 2})>f \rq \rq (0)>f(-\frac{1}{2})$

例4

若 $f(x)$ 在 $x = x_0$ 处连续，且 $\lim\limits_{x \to x_0}\dfrac{f(x)}{x - x_0} = A$ ，则 $f(x_0) = 0$ 且 $f \rq (x_0) = A$

(30讲例1.4.5)

$\sec x$ 的导数

$\begin{aligned} (\sec x) \rq =& (\dfrac{1}{\cos x}) \rq \\\\ =& \dfrac{-(\cos x) \rq}{\cos ^ 2 x} \\\\ =& \dfrac{\sin x}{\cos ^ 2 x} \\\\ =& \tan x \sec x \end{aligned}$

同理可得：$(\csc x)\rq = -\cot x \csc x$ 。

$\tan x$ 的导数

$\begin{aligned} (\tan x) \rq =& (\dfrac{\sin x}{\cos x}) \rq \\\\ =& \dfrac{(\sin x) \rq \cos x - \sin x (\cos x) \rq}{\cos ^ 2 x} \\\\ =& \dfrac{\cos ^ 2 x + \sin ^ 2 x}{\cos ^ 2 x} \\\\ =& \sec ^ 2 x \end{aligned}$

同理可得：$(\cot x)\rq = -\csc ^ 2 x$ 。