2-3-微分中值定理

函数极值

设 f(x)f(x) 在 (a,b)(a,b) 内有定义，x0∈(a,b)x_0 \in (a,b) ，如果存在点 x0x_0 的某个邻域 O(x0,δ)⊂(a,b)O(x_0, \delta) \subset (a, b) ，使得

f(x)⩽f(x0),x∈O(x0,δ)f(x) \leqslant f(x_0) , x \in O(x_0, \delta)

则称 x0x_0 是 f(x)f(x) 的一个极大值点， f(x0)f(x_0) 称为相应的极大值。类似地可以定义 f(x)f(x) 的极小值点和极小值。在不需要区分极大和极小的时候，统称为极值点和极值。

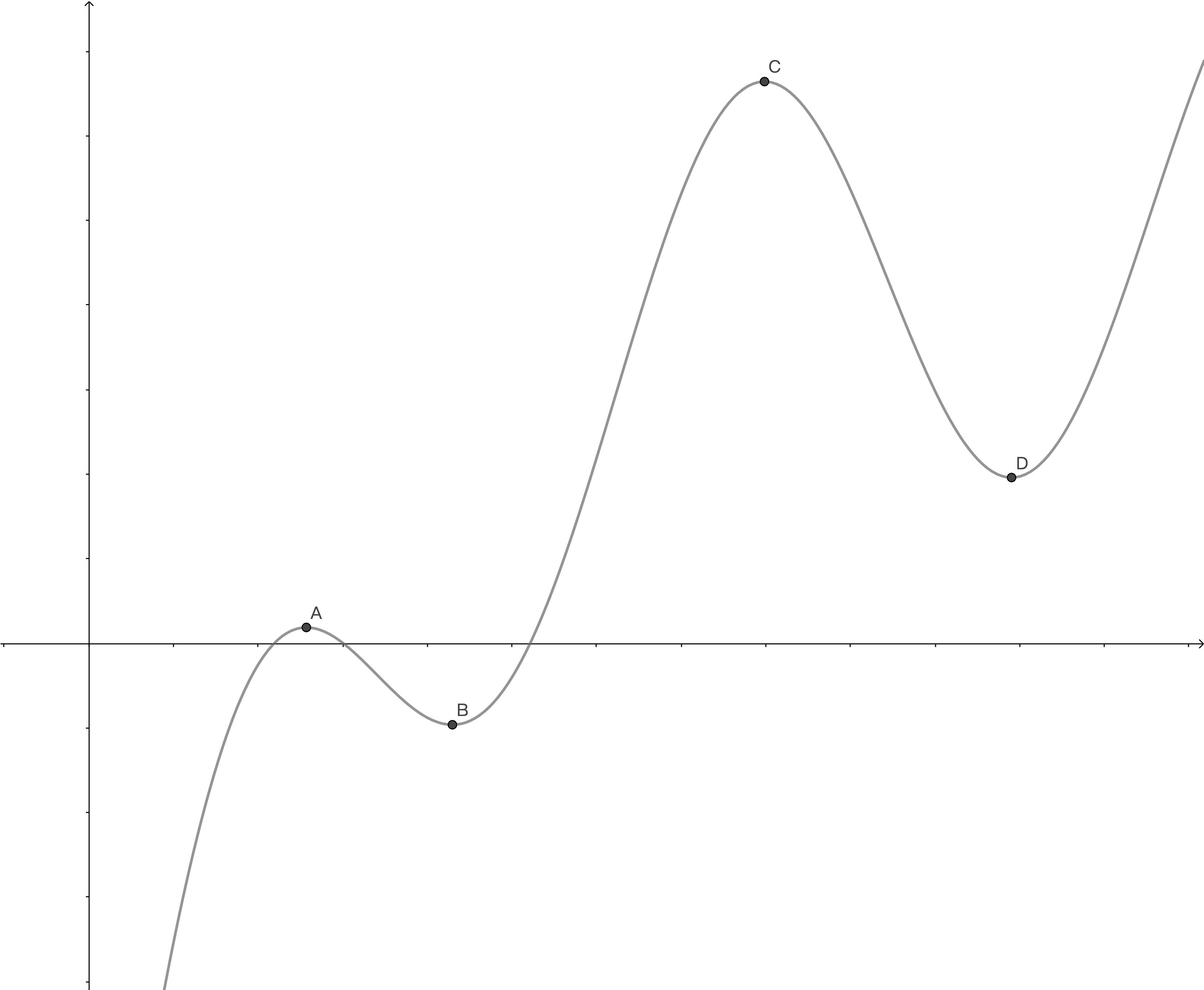
其中 A,CA,C 是极大值点， B,DB,D 是极小值点。

费曼引理

设 x0x_0 是 f(x)f(x) 的一个极值点，且 f(x)f(x) 在 x0x_0 处导数存在，则：

f′(x0)=0f^{'}(x_0) = 0

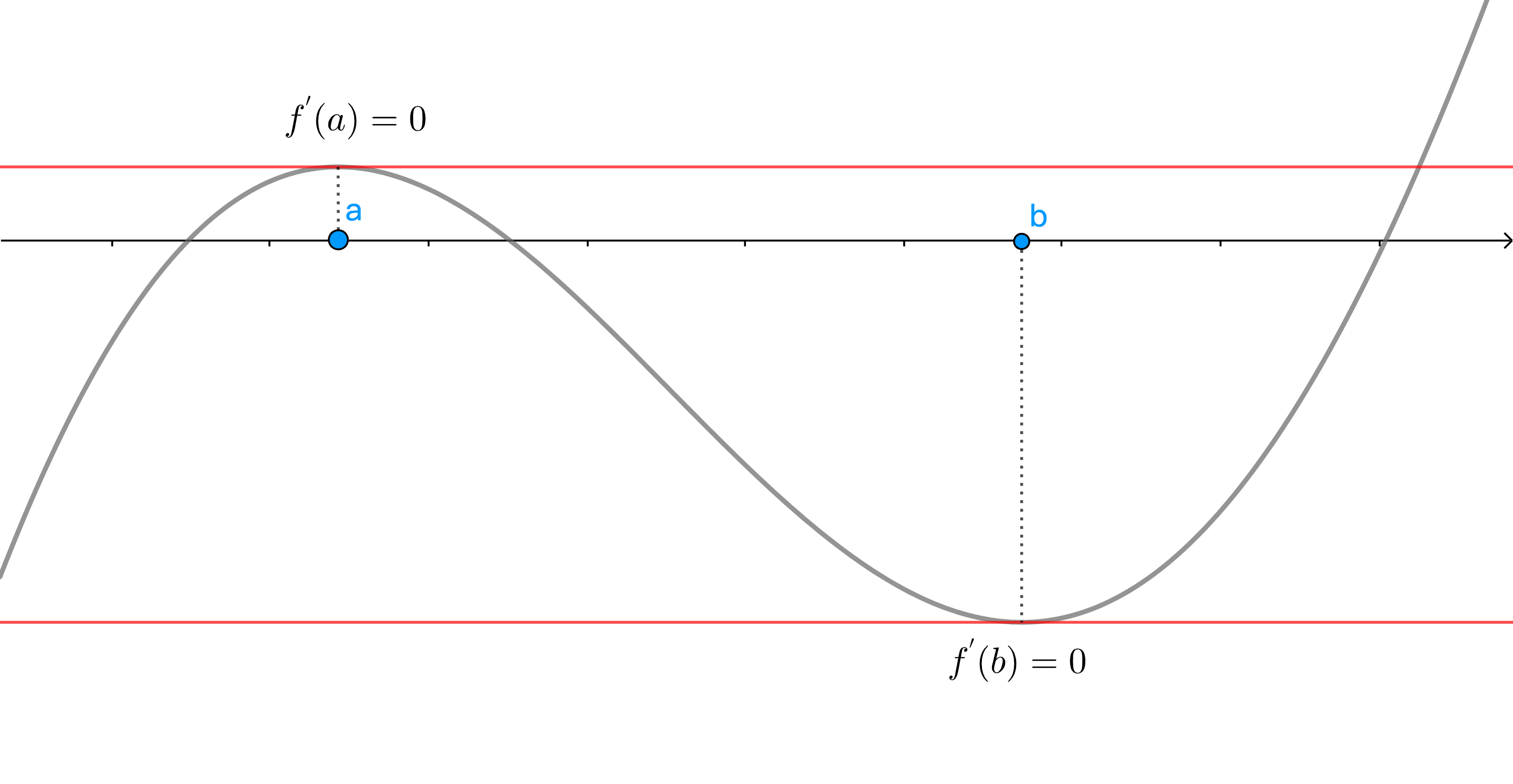
证明：不妨设 x0 是f(x) 的最大值点，有 f(x)⩽f(x0),x∈O(x0,δ) ，当 x<x0 时，有 f(x)−f(x0)x−x0⩾0 ，当 x>x0 时，有 f(x)−f(x0)x−x0⩽0 ；因为 f(x) 在 x0 处可导，且 f−′(x0)=lim⁡x→x0−f(x)−f(x0)x−x0⩾0 ，f+′(x0)=lim⁡x→x0+f(x)−f(x0)x−x0⩽0 ，即：f′(x0)=0.同理可证 x0 为极小值的情况。\begin{aligned} \text{证明：} \\\\ &\text{不妨设 } x_0 \text{ 是} f(x) \text{ 的最大值点，有 } f(x) \leqslant f(x_0) , x \in O(x_0, \delta) \text{ ，} \\\\ &\text{当 } x \lt x_0 \text{ 时，有 } \dfrac{f(x) - f(x_0)}{x - x_0} \geqslant 0 \text{ ，当 } x \gt x_0 \text{ 时，有 } \dfrac{f(x) - f(x_0)}{x - x_0} \leqslant 0 \text{ ；} \\\\ &\text{因为 } f(x) \text{ 在 } x_0 \text{ 处可导，且 } \\\\ &f^{'}_-(x_0) = \lim\limits_{x \to x_0^-}\dfrac{f(x) - f(x_0)}{x - x_0} \geqslant 0 \text{ ，} f^{'}_+(x_0) = \lim\limits_{x \to x_0^+}\dfrac{f(x) - f(x_0)}{x - x_0} \leqslant 0 \text{ ，} \\\\ &\text{即：} f^{'}(x_0) = 0 .\\\\ &\text{同理可证 } x_0 \text{ 为极小值的情况。} \end{aligned}

费曼引理的几何意义： 若在函数极值点处存在切线，则该切线一定平行于 xx 轴。

Rolle定理

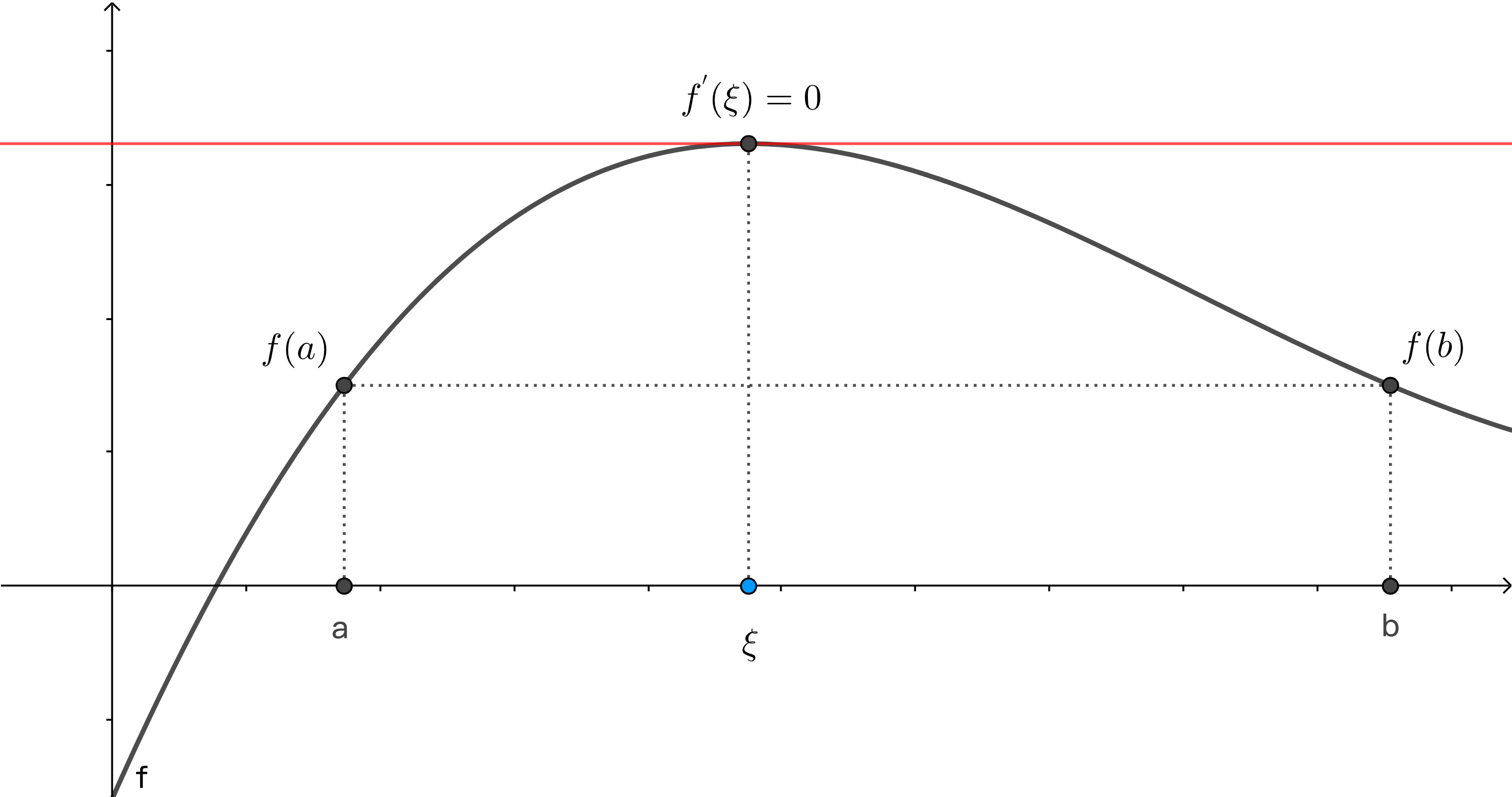
设函数 f(x)f(x) 在闭区间 [a,b][a, b] 上连续，开区间 (a,b)(a, b) 内可导，且 f(a)=f(b)f(a) = f(b) ，则至少存在一点 ξ∈(a,b)\xi \in (a, b) ，使得

f′(ξ)=0.f^{'}(\xi) = 0.

证明：设 M,m 分别是函数 f(x) 在 [a,b] 上的最大值和最小值，由闭区间上连续函数的性质，存在 ξ,η∈[a,b] ，使得 f(ξ)=M,f(η)=m.若M=m ，则 f(x) 在 [a,b] 上恒为常数，结论显然成立。由 M=f(ξ)>f(a)=f(b) ，显然 ξ∈(a,b) 是极大值点，由费曼引理 f′(ξ)=0.\begin{aligned} & \text{证明：} \\\\ & \text{设 } M,m \text{ 分别是函数 } f(x) \text{ 在 } [a, b] \text{ 上的最大值和最小值，} \\\\ & \text{由闭区间上连续函数的性质，存在 } \xi,\eta\in [a,b] \text{ ，使得 } f(\xi) = M,f(\eta) = m. \\\\ & \text{若} M = m \text{ ，则 } f(x) \text{ 在 } [a,b] \text{ 上恒为常数，结论显然成立。} \\\\ & \text{由 } M = f(\xi) \gt f(a) = f(b) \text{ ，显然 } \xi \in (a,b) \text{ 是极大值点，} \\\\ & \text{由费曼引理 } f^{'}(\xi) = 0. \end{aligned}

罗尔定理的几何意义

拉格朗日中值定理

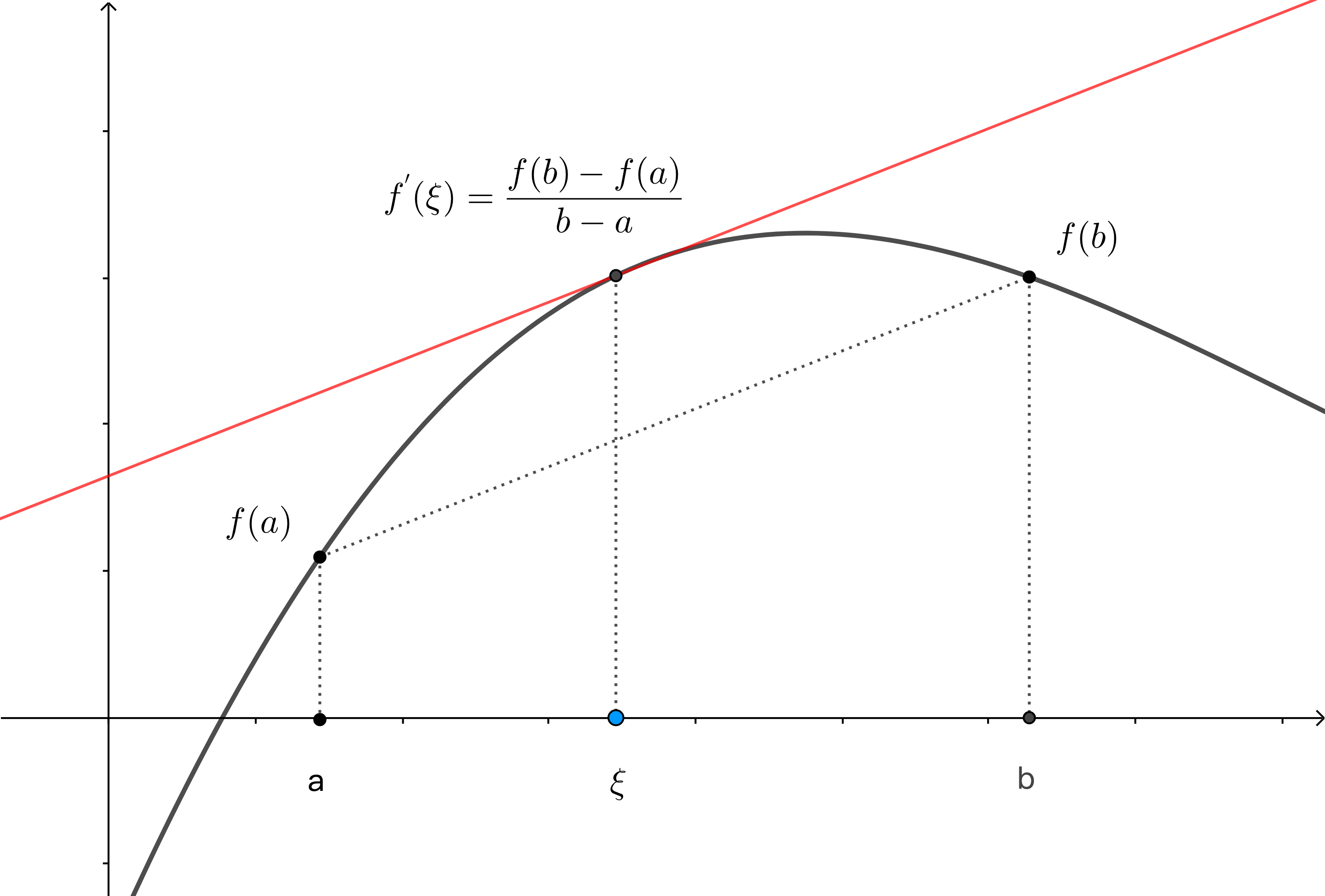
设函数 f(x)f(x) 在闭区间 [a,b][a, b] 上连续，开区间 (a,b)(a, b) 内可导，则至少存在一点 ξ∈(a,b)\xi \in (a, b) ，使得

f′(ξ)=f(b)−f(a)b−a.f^{'}(\xi) = \dfrac{f(b) - f(a)}{b - a}.

证明：设 φ(x)=f(x)−f(a)−f(b)−f(a)b−a(x−a),x∈[a,b],由于 f(x) 在闭区间 [a,b] 上连续，开区间 (a,b)内可导，因此 φ(x) 也在闭区间 [a,b] 上连续，开区间 (a,b)内可导，且 φ(a)=φ(b)=0,于是由罗尔定理，至少存在一点 ξ ，使得 φ′(ξ)=0,即 φ′(ξ)=f′(ξ)−f(b)−f(a)b−a=0,因此 f′(ξ)=f(b)−f(a)b−a.\begin{aligned} & \text{证明：} \\\\ & \text{设 } \varphi (x) = f(x ) - f(a) - \dfrac{f(b) - f(a)}{b - a}(x -a), x\in[a,b], \\\\ & \text{由于 } f(x) \text{ 在闭区间 } [a,b] \text{ 上连续，开区间 } (a,b) \text{内可导，} \\\\ & \text{因此 } \varphi (x) \text{ 也在闭区间 } [a,b] \text{ 上连续，开区间 } (a,b) \text{内可导，且 } \varphi(a) = \varphi(b) = 0, \\\\ & \text{于是由罗尔定理，至少存在一点 } \xi \text{ ，使得 } \varphi^{'}(\xi) = 0, \\\\ & \text{即 } \varphi^{'}(\xi) = f^{'}(\xi) - \dfrac{f(b) - f(a)}{b - a} = 0, \\\\ & \text{因此 } f^{'}(\xi) = \dfrac{f(b) - f(a)}{b - a}. \end{aligned}

拉格朗日中值定理的几何意义

柯西中值定理

设 f(x)f(x) 和 g(x)g(x) 都在闭区间 [a,b][a, b] 上连续，开区间 (a,b)(a,b) 内可导，且对于任意的 x∈(a,b),g′(x)≠0x \in (a,b),g^{'}(x)\neq 0 。则至少存在一点
ξ∈(a,b)\xi \in (a,b) ，使得

f′(ξ)g′(ξ)=f(b)−f(a)g(b)−g(a)\dfrac{f^{'}(\xi)}{g^{'}(\xi)} = \dfrac{f(b) - f(a)}{g(b) - g(a)}

当 g(x)=xg(x) = x 时，即为拉格朗日公式，所以拉格朗日中值定理是柯西中值定理的特殊情况。

一阶导数与单调性的关系

设函数 f(x)f(x) 在区间 II 上可导，则 f(x)f(x) 在 II 上单调增加的充分必要条件是：对于任意的 x∈Ix \in I 有 f′(x)⩾0f^{'}(x) \geqslant 0 ；
特别地，若对于任意 x∈Ix \in I 有 f′(x)>0f^{'}(x) \gt 0 ，则 f(x)f(x) 在 II 上严格单调增加。

证明：充分性：∀x1,x2∈I(x1<x2),∃ξ∈(x1,x2) ，使得 f(x2)−f(x1)=f′(ξ)(x2−x1).由于 x2−x1>0 ，因此 f(x2)−f(x1) 与 f′(ξ) 同号。所以，当 f′(ξ)⩾(>)0,f(x) 在 I 上单调增加（严格单调增加）。必要性：∀x∈I ，由于 f(x) 在 I 单调增加，所以对于任意的 x0∈I(x0≠x) 有f(x0)−f(x)x0−x⩾0,令 x0→x ，于是得到 f′(x)⩾0.\begin{aligned} \text{证明：} & \\\\ & \text{充分性：} \\\\ & \forall x_1,x_2\in I (x_1 \lt x_2), \exists \xi \in (x_1,x_2) \text{ ，使得 } \\\\ & f(x_2) - f(x_1) = f^{'}(\xi)(x_2-x_1). \\\\ & \text{由于 } x_2 - x_1 \gt 0 \text{ ，因此 } f(x_2) - f(x_1) \text{ 与 } f^{'}(\xi) \text{ 同号。} \\\\ & \text{所以，当 } f^{'}(\xi) \geqslant (\gt) 0 , f(x) \text{ 在 } I \text{ 上单调增加（严格单调增加）。} \\\\ & \text{必要性：} \\\\ & \forall x \in I \text{ ，由于 } f(x) \text{ 在 } I \text{ 单调增加，所以对于任意的 } x_0\in I (x_0 \neq x) \text{ 有} \\\\ & \dfrac{f(x_0) - f(x)}{x_0 - x} \geqslant 0, \\\\ & \text{令 } x_0 \to x \text{ ，于是得到 } f^{'}(x) \geqslant 0. \end{aligned}

类似地可得到在 II 上 f′(x)⩽0f^{'}(x) \leqslant 0 （或 f′(x)<0f^{'}(x) \lt 0）与 f(x)f(x) 在 II 上单调减少（或严格单调减少）之间的关系。

二阶导数与凹凸性的关系

2-线性空间
2-2-微分